Datové struktury založené na stromech

Note	Stromové datové struktury (binární vyhledávací stromy, B-stromy, červeno-černé stromy, haldy), související operace a jejich složitost. Typické implementace, příklady použití. IB002

Warning

Obrázky v této otázce kreslené rukou byly sprostě ukradeny Dominice Krejčí z https://github.com/Krejdom/school_notes. Snad jen dočasně.

Strom je abstraktní datová struktura, o které se dá uvažovat jako o množině uzlů, které mají právě jednoho rodiče a konečný počet dětí. Výjimkou je kořen, který nemá rodiče. Hodnotám v uzlech se říká klíče.

Binární strom: Strom, kde každý uzel má nejvýše dvě děti.
Výška uzlu $n$: Počet hran nejdelší cesty z $n$ do některého z poddaných listů.

Binární vyhledávací strom (BVS)

Binární strom, kde pro každý uzel $n$ platí

klíče uzlů v jeho levém podstromě jsou menší nebo rovny klíči uzlu $n$ ,
klíče uzlů v jeho pravém podstromě jsou větší než klíč uzlu $n$ .

Je teoretickým základem pro složitejší stromové struktury.

Příklad

Inorder průchod

def inorder(node):
    inorder(node.left)
    print(node.key)
    inorder(node.right)

Preorder průchod

def preorder(node):
    print(node.key)
    preorder(node.left)
    preorder(node.right)

Postorder průchod

def postorder(node):
    postorder(node.left)
    postorder(node.right)
    print(node)

Následník uzlu $n$

Je uzel obsahující nejmenší klíč větší než n.key.

Předchůdce uzlu $n$

Je uzel obsahující největší klíč menší než n.key.

Úplný binární strom

Všechna jeho patra, kromě nejnižšího jsou zaplňena. V nejnižším patře jsou listy nasoukané vlevo.

AVL-strom

BVS, kde délka nejdelší větve levého a pravého podstromu každého uzlu se liší nejvýše o 1.

Implementace

Každý uzel má v paměti vlastní strukturu/objekt a obsahuje:

klíč (hodnotu),
ukazatel na levého syna,
ukazatel na pravého syna.

Binární vyhledávání: Porovnáváme hodnotu s klíčem a jdeme buď doleva nebo doprava.
Minimum a maximum: Jde úplně vlevo pro minimum, úplně vpravo pro maximum.
Následník: Pokud má uzel pravý podstrom, následník je jeho minimem. Pokud nemá pravý podstrom, hledáme prvního předka, v jehož levém podstromu se uzel nachází.
Insert: Binární vyhledávání, ale na prázdné místo dáme uzel.
Remove: Binární vyhledávání, ale nalezený uzel smažeme. Pokud měl děti, najdeme jeho následníka a dosadíme ho za smazaný uzel.

Halda (heap)

Strom splňující vlastnost haldy, t.j. klíč každého uzllu je větší než klíče jeho dětí. Kořen má největší klíč.

Používá se např. k implementaci prioritní fronty a v heap sortu.

Note	Z historických důvodů se slovem ,,halda'' označuje také kus paměti určený pro dynamickou alokaci. V dnešní době tam už souvislost, zdá se, není.

Binární halda: Úplný binární strom splňující vlastnost haldy.
Maximová halda: Kořen má největší klíč.
Minimová halda: Kořen má nejmenší klíč.
Heap sort: Vybudujeme haldu ( $O (n)$ ) a postupně z ní odstraňujeme kořen ( $O (1)$ ), což vždy následuje oprava haldy ( $O (lo g (n))$ ). Celková složitost je $O (n \cdot lo g (n))$ .

Implementace

Binární haldu lze implementovat pomocí pole:

Kořen je na indexu 1.
Levý syn uzlu $i$ je na $2 i$ .
Pravý syn uzlu $i$ je na $2 i + 1$ .

Note	Indexuješ-li od nuly, pak je to $2 i - 1$ a $2 i + 2$

Rodič uzlu $k$ se nachází na $⌊ \frac{k}{2} ⌋$ (při indexování od 1).

Červeno-černý strom

Binární vyhledávací strom, který ma uzly obarvené červenou nebo černou barvou a splňuje následující podmínky

kořen je černý,
listy neobsahují klíče (obsahují null) a jsou černé,
pokud je uzel červený, má černého rodiče,
pro každý uzel platí, že všechny cesty z něj do listu obsahují stejný počet černých uzlů.

Používá se k výpočtu ranku prvku (počet menších prvků zvýšený o jedna), při implementaci asociativní paměti a AVL-stromů.

Černá výška uzlu $n$: Počet černých uzlů na cestě z $n$ do některého z poddaných listů $n$ . Pokud je $n$ černý, nepočítá se.

Každý uzel výšky $h$ má černou výšku alespoň $\frac{h}{2}$ .

Červeno-černý strom s $n$ vnitřními uzly má výšku nejvýše $2 \cdot lo g_{2} (n + 1)$ .

Implementace

Jako BVS, ale každý uzel obsahuje kromě klíče a ukazatelů na potomky také barvu a ukazatel na rodiče.

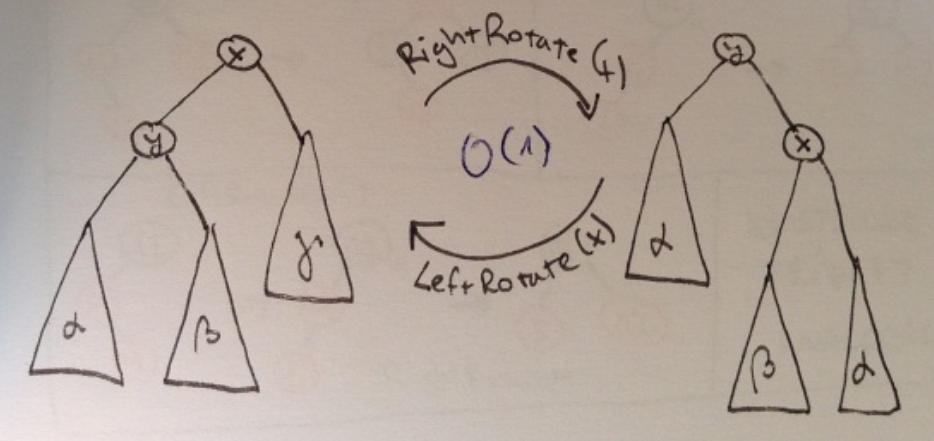
Rotace

Používájí se k opravě následků přidávání a odebírání uzlů.

Insert

Uzel vložíme do stromu stejně jako do BVS a obarvíme ho červeně. A strom opravíme. Jelikož oprava má konstantní složitost, je složitost stejná jako u BVS, t.j. $O (lo g (n))$ .

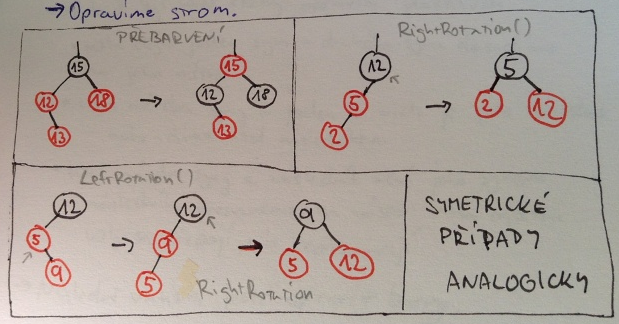
Delete

Uzel ostraníme stejně jako u BVS. Navíc, pokud byl červený, tak se nic neděje, ale pokud byl černý a

měl jednoho syna, tak jeho syn zaujme jeho místo.
měl dva syny a jeden z nich je jeho následník, tak jeho místo zaujme syn-následník
měl dva syny a ani jeden z nich nebyl jeho následník, následník zaujme jeho místo a stane se otčímem obou synů. U původních dětí se řeší stejná situace jako tady.

Následně opravíme barvy.

B-strom

B-strom stupně $m$ je strom, kde platí

každý uzel má nejvýše $m$ dětí,
každý vnitřní uzel (kromě kořene) má alespoň $⌈ \frac{m}{2} ⌉$ dětí,
kořen má alespoň 2 děti, pokud není listem,
vnitřní uzel s $k$ dětmi obsahuje $k - 1$ klíčů,
všechny listy mají stejnou hloubku a jejich klíče jsou null.

Klíče ve vnitřních uzlech vymezují intervaly, do kterých spadají jejich postromy.

Note	V IB002 má B-strom nejméně $t$ dětí a nejvýše $2 t$ dětí. Hodnota $t$ je minimální stupeň stromu.

B-strom s $n \geq 1$ klíči a minimálním stupněm $t \geq 2$ má hloubku nejvýše $h \leq lo g_{t} (\frac{n + 1}{2})$ .

Využívá se v databázích a je základem B+ stromu.

Plný uzel: Má $m$ dětí.

Implementace

Struktura/objekt reprezentující uzel v paměti obsahuje:

počet klíčů,
klíče v neklesajícím pořadí,
ukazatele na děti.

Vyhledávání: Analogické binárnímu vyhledávání.
Insert: Vyhledáváním najdeme uzel, kam by klíč měl patřit. Pokud je uzel plný, rozdělíme ho na dva. Pokud tím přeplníme rodiče, rozdělíme i rodiče, atd.
Preemptivní dělení: Optimalizace přístupu na disk. Pokud při průchodu stromem narazíme na plný uzel, pro jistotu ho rozdělíme.
Delete: Mazání probíhá vždy v listu. Pokud mazaný klíč není v listu, nahradíme ho za následníka, přesuneme ho do listu, a pak ho teprve smažeme.
Preemptivní slučování: Pokud narazíme na uzel, co má $t - 1$ uzlů, zvýšíme počet přesunem vhodného klíče na $t$ .

Složitost základních operací

Struktura insert remove search max min next prev

Struktura	`insert`	`remove`	`search`	`max`	`min`	`next`	`prev`
Binární vyhledávací strom	$O (n)$	$O (n)$	$O (n)$	$O (n)$	$O (n)$	$O (n)$	$O (n)$
Binární maximová halda	$O (l o g (n))$	$O (l o g (n))$ pro maximum	$O (n)$	$O (1)$	$O (n)$	$O (n)$	$O (n)$
Červeno-černý strom	$O (l o g (n))$	$O (l o g (n))$	$O (l o g (n))$	$O (l o g (n))$	$O (l o g (n))$	$O (l o g (n))$	$O (l o g (n))$
B-strom	$O (t \cdot l o g_{t} (n))$	$O (t \cdot l o g_{t} (n))$	$O (t \cdot l o g_{t} (n))$

Binární vyhledávací strom

$O (n)$

Binární maximová halda

$O (l o g (n))$

$O (l o g (n))$ pro maximum

$O (n)$

$O (1)$

$O (n)$

Červeno-černý strom

$O (l o g (n))$

B-strom

$O (t \cdot l o g_{t} (n))$