Trénink

Přehled

Likelihood
Linear regression
Logistic regression
Gradient descent
Error functions

Likelihood

Ve statistice jsou dva pojmy:

Probability $P$ , $p$: Říká, jaká je pravděpodobnost, že daný jev se v našem modelu stane.
Likelihood $L$: Říká, jak dobře náš model (rozdělení pravděpodobnosti náhodné veličiny) sedí na naměřená data.

Note	Pravděpodobnost je funkce jevů. Likelihood je funkce parametrů modelu.

Note	Likelihood nemusí nutně vracet čísla z intervalu $[0, 1]$ .

Jak to souvisí s trénováním neuronek? Neuronka je model, kde váhy neuronů jsou parametry. Při učení neuronek je naším cílem maximalizovat likelihood, jakožto míru toho, že naše síť sedí na "naměřená data", training set $T$ . Tomuhle přístupu se říká maximum likelihood principle.

Training set $T$: je množina $p$ samplů, kde $x \in R^{∣ X ∣}$ jsou vstupní vektory a $d \in R^{∣ Y ∣}$ jejich očekáváné výstupy.

$T = {(x_{1}, d_{1}), (x_{2}, d_{2}), ..., (x_{p}, d_{p})}$

Linear regression

Linear regression je metoda, kdy na základě naměřených dat hledáme linární model. Tedy výstup závisí na vstupech (Ano, může být víc než jeden.) lineárně. Uvažme neuron, kde:

vnitřní potenciál $ξ = w \cdot x + b = b + \sum_{i = 1}^{n} w_{i} x_{i}$ ,
aktivační funkce $σ (ξ) = ξ$ je pass-through,
výstup je jedno číslo $y = σ (ξ) = w \cdot x + b$ ,
množina $D = {(x_{1}, d_{1}), (x_{2}, d_{2}), ..., (x_{p}, d_{p})}$ je trénovací set.

Předpokládáme, že každý očekávaný výstup byl generován takto:

d_{k} N [0, \overset{σ}{ˉ}^{2}] (ϵ_{k}) = (w \cdot x_{k} + b) + ϵ_{k} = \frac{1}{σ ˉ 2 π} \cdot exp (- \frac{( ϵ _{k} - 0 ) ^{2}}{2 σ ˉ ^{2}})

kde $x$ je vstup, $ϵ_{k}$ je normálně distribuovaný šum se střední hodnotou 0, a $w$ , $b$ a $\overset{σ}{ˉ}^{2}$ jsou parametry modelu.

Note	Směrodatná odchylka $\overset{σ}{ˉ}$ není aktivační funkce $σ$ .

Dále předpokládáme, že šumy $ϵ_{1}, ..., ϵ_{p}$ byly vygenerovány vzájemně nezávisle.

Naším cílem je najít hodnoty pro červené parametry takové, že maximalizují likelihood:

L (w, b, \overset{σ}{ˉ}^{2}) = p (d_{1}, ..., d_{p} ∣ w, b, \overset{σ}{ˉ}^{2}) = k = 1 \prod p N [b + w \cdot x_{k}, \overset{σ}{ˉ}^{2}] (d_{k}) = k = 1 \prod p \frac{1}{σ ˉ ^{2} 2 π} exp (- \frac{( d _{k} - b + w \cdot x _{k} ) ^{2}}{2 σ ˉ})

Kde $p$ je hustota pravděpodobnosti, podle které byly očekávané hodnoty $d_{1}, ..., d_{k}$ vygenerovány za předpokladu fixních $b, w, σ^{2}, x_{1}, ..., x_{p}$ .

Všimni si, že je tu podobné normální rozdělení jako u $ε_{k}$ , ale střední hodnotu takovou, aby generovalo $d_{k}$ , pokud náš model funguje.

Note	Bez předpokladu normálnosti a vzájemné nezávislosti šumů by to nešlo.

Věta: Parametry $(b, w)$ maximalizují likelihood $L (b, w, \overset{σ}{ˉ}^{2})$ pro libovolné $\overset{σ}{ˉ}^{2}$ , právě když $(b, w)$ minimalizují squared error $E (b, w) = \sum_{k = 1}^{p} (d_{k} - b + w \cdot x_{k})^{2}$ .

Note	Maximalizace/minimalizace $(b, w)$ je na odchylce šumu $\overset{σ}{ˉ}^{2}$ je nezávislá. $\overset{σ}{ˉ}^{2}$ je maximální, když $σ^{2} = \frac{1}{p} \sum_{k = 1}^{p} (d_{k} - b + w \cdot x_{k})^{2}$ .

Důkaz: $LL (w, b, \overset{σ}{ˉ}^{2}) = lo g p (d_{1}, ..., d_{p} ∣ w, b, \overset{σ}{ˉ}^{2}) = lo g k = 1 \prod p \frac{1}{σ ˉ ^{2} 2 π} exp (- \frac{( d _{k} - b + w \cdot x _{k} ) ^{2}}{2 σ ˉ}) = k = 1 \sum p lo g \frac{1}{σ ˉ 2 π} Space + Space \frac{1}{2 σ ˉ ^{2}} k = 1 \sum p - (d_{k} - b + w \cdot x_{k})^{2}$

Jelikož maximalizováním logistic likelihood $LL$ , maximalizujeme i $L$ , pak $L$ je maximální (nezávisle na volbě $\overset{σ}{ˉ}^{2}$ ), pokud $E (b, w)$ je minimální.

Logistic regression

Logistic regression je metoda, kdy na základě naměřených dat hledáme model, kde vztah mezi vstupy a výstupy odpovídá funkci logistic sigmoid. Výsledkem je klasifikace (pravděpodobnost) mezi dvěma třídami 0 a 1. Uvažme neuron, kde:

vnitřní potenciál $ξ = w \cdot x + b = b + \sum_{i = 1}^{n} w_{i} x_{i}$ ,
aktivační funkce $σ (ξ) = \frac{1}{1 + e ^{- λ \cdot ξ}}$ je logistic sigmoid,
výstup je jedno číslo $y = σ (ξ)$ z intervalu $[0, 1]$ ,
množina $D = {(x_{1}, d_{1}), (x_{2}, d_{2}), ..., (x_{p}, d_{p})}$ je trénovací set.

Note	Odds (poměr pravděpodobností) je poměr pravděpodobnosti toho, že jev nastane, k pravděpodobnosti toho, že jev nenastane. Tedy pokud má jev pravděpodobnost $P$ , pak odds jsou $\frac{P}{1 - P}$ . (Čitatel a jmenovatel dají tedy v součtu 1.) Logaritmus odds nazýváme logit.

Logistic sigmoid

Proč použít právě logistic sigmoid? Dejme tomu, že opravdová šance, že klasifikovaný objekt patří do třídy 1, je $\overset{y}{^}$ , pak:

odds (\overset{y}{^}) = \frac{y ^}{1 - y ^}

což připomíná exponenciální funkci:

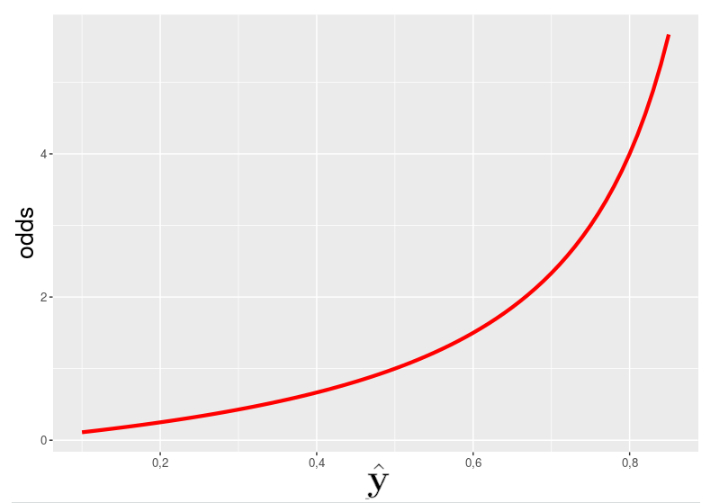
Když ale na obě strany aplikujeme logaritmus:

logit (\overset{y}{^}) = lo g \frac{y ^}{1 - y ^}

připomíná spíše lineární funkci:

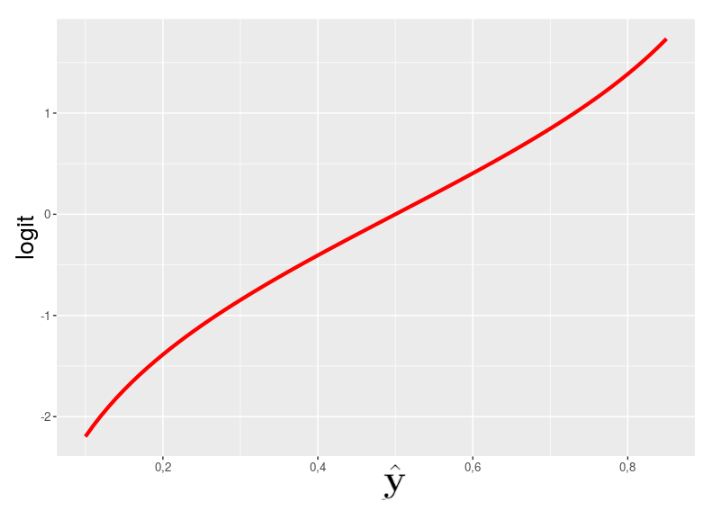
Ale… vnitřní potenciál je taky lineární, ne?

lo g \frac{y ^}{1 - y ^} lo g \frac{1 - y ^}{y ^} \frac{1 - y ^}{y ^} 1 - \overset{y}{^} 11 \overset{y}{^} \approx ξ = w \cdot x \approx - w \cdot x \approx e^{- w \cdot x} \approx e^{- w \cdot x} \cdot \overset{y}{^} \approx e^{- w \cdot x} \cdot \overset{y}{^} + \overset{y}{^} \approx \overset{y}{^} (e^{- w \cdot x} + 1) \approx \frac{1}{1 + e ^{- w \cdot x}}

Takže klasifikaci vstupu jako 0 nebo 1 ( $\overset{y}{^}$ ) aproximujeme pomocí funkce logistic sigmoid, pravděpodobností $y$ .

Minimalizace likelihoodu

Likelihood v případě binární klasifikace si můžeš představit na hodech mincí (se stranami 0 a 1). Nechť je $y$ je odhad pravděpodobnosti tvého logistic sigmoid modelu, že spadne 1, a $T = {1, 1, 0, 0, 1}$ tvůj dataset. Pak likelihood, že tvůj model vygeneruje právě tenhle data set je:

L = y \cdot y \cdot (1 - y) \cdot (1 - y) \cdot y

Když upustíme od příkladu s mincí, pak pro obecnou binarní klasifikaci s datasetem $T$ :

L = k = 1 \prod p y_{k}^{d_{k}} \cdot (1 - y_{k})^{(1 - d_{k})}

Násobení se nám nelíbí, takže stejně jako u linear regression budeme maximalizovat logistic likelihood:

LL = lo g k = 1 \prod p y_{k}^{d_{k}} \cdot (1 - y_{k})^{(1 - d_{k})} = k = 1 \sum p lo g (y_{k}^{d_{k}} \cdot (1 - y_{k})^{(1 - d_{k})}) = k = 1 \sum p d_{k} lo g y_{k} + (1 - d_{k}) lo g (1 - y_{k})

Podobně jako u linear regression chceme spíš minimalizovat nějakou error function $E$ . V případě logistic regression volíme binary cross-entropy:

E (w) = - LL = - k = 1 \sum p d_{k} lo g y_{k} + (1 - d_{k}) lo g (1 - y_{k})

Gradient descent

Gradient descent je algoritmus, který nám umožňuje najít váhy $w$ takové, že hodnota error function $E$ bude minimální. Jdeme proti směru gradientu (vektoru parciálních derivací $E$ ). Gradient udává směr, kterým funkce roste nejrychleji:

\nabla E (w) = (\frac{\partial E}{\partial w _{0}} (w), ..., \frac{\partial E}{\partial w _{n}} (w))

Gradient descent funguje iterativně, přižemž v 0-té iteraci jsou váhy $w^{(0)}$ inicializovány náhodnými čísly blízko 0. Pro následující iterace pak platí:

w^{(t + 1)} Δ w^{(t)} = w^{(t)} + Δ w^{(t)} = - ε \cdot \nabla E (w^{(t)})

ADALINE

ADALINE je jeden neuron ze 60. let, co dělá lineární regresi. Pokud za $E$ zvolíme squared error $E = \frac{1}{2} \sum_{k = 1}^{p} (w \cdot x - d_{k})^{2}$ :

\frac{\partial E}{\partial w _{l}} \nabla E (w) = \frac{1}{2} k = 1 \sum p \frac{\partial}{\partial w _{l}} (i = 0 \sum n w_{i} x_{ki} - d_{k})^{2} = \frac{1}{2} k = 1 \sum p 2 (i = 0 \sum n w_{i} x_{ki} - d_{k}) \cdot \frac{\partial}{\partial w _{l}} (i = 0 \sum n w_{i} x_{ki} - d_{k}) = \frac{1}{2} k = 1 \sum p 2 (i = 0 \sum n w_{i} x_{ki} - d_{k}) (i = 0 \sum n \frac{\partial}{\partial w _{l}} w_{i} x_{ki} - \frac{\partial E}{\partial w _{l}} d_{k}) = k = 1 \sum p (w \cdot x_{k} - d_{k}) x_{k l} = k = 1 \sum p (w \cdot x_{k} - d_{k}) x_{k}

Note	Věta (Widrow & Hoff) Pokud $ε (t) = \frac{1}{2}$ , pak posloupnost $w^{(0)}$ , $w^{(1)}$ , … konverguje ke globálnímu minimum $E$ .

Multilayer Perceptron

U feed-forward sítí jakou je MLP, se pro výpočet gradientu používá backpropagation:

w_{ji}^{(t + 1)} Δ w_{ji}^{(t)} \frac{\partial E}{\partial w _{ji}} \frac{\partial E _{k}}{\partial w _{ji}} = w_{ji}^{(t)} + Δ w_{ji}^{(t)} = - ε (t) \cdot \frac{\partial E}{\partial w _{ji}} (w^{(t)}) = k = 1 \sum p \frac{\partial E _{k}}{\partial w _{ji}} = \frac{\partial E _{k}}{\partial y _{j}} \cdot \frac{\partial y _{j}}{\partial ξ _{j}} \cdot \frac{\partial ξ _{j}}{\partial w _{ji}} = \frac{\partial E _{k}}{\partial y _{j}} \cdot σ_{j}^{'} (ξ_{j}) \cdot y_{i}

Za předpokladu, že $E$ je squared error, pak:

\frac{\partial E _{k}}{\partial y _{j}} = ⎩ ⎨ ⎧ y_{j} - d_{kj} \sum_{r \in j^{\to}} \frac{\partial E _{k}}{\partial y _{r}} \cdot \frac{\partial y _{r}}{\partial ξ _{r}} \cdot \frac{\partial ξ _{r}}{\partial y _{j}} = \sum_{r \in j^{\to}} \frac{\partial E _{k}}{\partial y _{r}} \cdot σ_{r}^{'} (ξ_{r}) \cdot w_{r j} pokud j \in Y; jinak .

Představ si, že při derivaci $E_{k}$ podle $y_{j}$ , kde $j$ není výstup, tě zajímají jen členy $y_{r}$ , protože jen při vyhodnocení neuronů $r$ je hodnota $y_{j}$ potřeba, takže všechno ostatní se zderivuje na konstantu.

Note	Uvědom si, že tyhle $\frac{\partial E _{k}}{\partial y _{j}}$ derivace se počítají po vrstvách v obráceném pořadí než, když NN vyhodnocuješ. To znamená, že hodnotu $\frac{\partial E _{k}}{\partial y _{r}}$ už spočítanou máš, protože jsi ji počítal v minulé vrstvě.

Algoritmus pro výpočet

\frac{\partial E}{\partial w _{ji}}

Inicializuj $ε_{ji} := 0$ .
forward pass — vyhodnoť NN pro sample $k$ (t.j. $y_{j} (w, x_{k})$ pro všechny $j \in Z$ )
backward pass — od konce pro každou vrstvu spočítej $\frac{\partial E _{k}}{\partial y _{j}}$
1. pokud $j \in Y$ , pak $\frac{\partial E _{k}}{\partial y _{j}} = y_{j} - d_{kj}$
2. pokud $j \in Z ∖ Y \cup X$ , a $j$ je v $l$ -té vrstvě, pak $\frac{\partial E _{k}}{\partial y _{j}} = \sum_{r \in j^{\to}} \frac{\partial E _{k}}{\partial y _{r}} \cdot σ_{r}^{'} (ξ_{r}) \cdot w_{r j}$
weight update — pro všechna $w_{ji}$ spočítej $\frac{\partial E _{k}}{\partial w _{ji}} := \frac{\partial E _{k}}{\partial y _{j}} \cdot σ_{j}^{'} (ξ_{j}) \cdot y_{i}$
$ε_{ji} := ε_{ji} + \frac{\partial E _{k}}{\partial w _{ji}}$
$ε_{ji}$ obsahuje výslednou hodnotu $\frac{\partial E}{\partial w _{ji}}$

Note	Tenhle algoritmus předpokládá za error function squared error a za $σ$ funkci, která fakt bere za parametr jen vnitřní potenciál jednoho neuronu a ne třeba celé vrstvy, jak to dělá softmax.

Note	Co se časové složitosti týče, tak je tenhle algoritmus lineární vzhledem k počtu vrstev NN. Nicméně tohle je jen jedna iterace, časovou složitost minimalizace gradientu nejde odhadnout.

Online Gradient Descent: Samply bereš po jednom $k$ , takže:

$Δ w^{(t)} = - ε (t) \cdot \nabla E_{k} (w^{(t)})$
Stochastic Gradient Descent (SGD): Sample nebereš po jednom ale po malých randomizovaných várkách — minibatchích $T$ :

$Δ w^{(t)} = - ε (t) \cdot k \in T \sum \nabla E_{k} (w^{(t)})$
Learning rate $ε$: Hyperparametr $0 < ε \leq 1$ ovlivňující rychlost učení. Může záviset na iteraci $t$ , pak je to funkce $ε (t)$ .
Epocha: Jeden průchod celým trénovacím setem.

Error functions

Přehled error functions v tomto kurzu:

Squared error

E (w) E_{k} (w) = k = 1 \sum p E_{k} (w) = \frac{1}{2} j \in Y \sum (y_{j} (w, x_{k}) - d_{kj})^{2}

Mean squared error

E (w) = \frac{1}{p} k = 1 \sum p E_{k} (w)

Binary cross-entropy

E (w) = - k = 1 \sum p d_{k} lo g y_{k} + (1 - d_{k}) lo g (1 - y_{k})

(Categorical) cross-entropy

E (w) = - \frac{1}{p} k = 1 \sum p j \in Y \sum d_{kj} ln (y_{j})

Používá se při multi-class classification (např. číslice v MNISTu). Klasifikační sítě zároveň prakticky vždy mají výstupní vrstvu s aktivační funkcí softmax, neboť pak pro váhy mezi předposlední a poslední, softmax vrstvou platí:

\frac{\partial E _{k}}{\partial w _{ji}} = \frac{\partial E _{k}}{\partial ξ _{j}} \cdot \frac{\partial ξ _{j}}{\partial w _{ji}} = (d_{kj} - y_{j}) \cdot y_{i}

Note	Pro vysvětlení, jak a proč tohle funguje, čti tohle.