Multilayer Perceptron (MLP)

Přehled

Notace
Aktivita
Důkazy
Výpočetní síla

Notace

MLP je feed-forward architektura NN, kde jsou neurony rozděleny do vrstev — jedné vstupní, jedné výstupní a libovolného počtu skrytých vrstev uprostřed. Input layer má index 0. Každý neuron v i-té vrstvě je napojen na každý neuron v (i + 1)-ní vrstvě.

$X$ — množina input neuronů
$Y$ — množina output neuronů
$Z$ — množina všech neuronů
Neurony mají indexy $i$ , $j$ , …
$ξ_{j}$ — vnitřní potenciál neuronu $j$ po skončení výpočtu
$y_{j}$ — výstup neuronu $j$ po skončení výpočtu
$x_{0} = 1$ — hodnota formálního jednotkového vstupu (kvůli biasům)
$w_{ji}$ — váha spojení z neuronu $i$ do neuronu $j$ (dst ← src)
$w_{j 0} = - b_{j}$ — bias — váha z formální jednotky do neuronu $j$
$j_{\leftarrow}$ — množina neuronů $i$ , jenž mají spojení do $j$ (j ← i)
$j^{\to}$ — množina neuronů $i$ , do nichž vede spojení z $j$ (j → i)

Aktivita

Pravidlo pro výběr neuronů při výpočtu: V i-tému kroku vezmi i-tou vrstvu.
Vnitřní potenciál neuronu $j$: $ξ_{j} = \sum_{i \in j_{\leftarrow}} w_{ji} y_{i}$
Aktivační funkce neuronu $j$: $σ_{j} : R \to R$ (třeba logistic sigmoid)
Stav nevstupního neuronu $j$: $y_{j} = σ_{j} (ξ_{j})$ resp. $y_{j} (w, x)$

Aktivační funkce

Unit step function

σ (ξ) = {10 ξ \geq 0; ξ < 0.

Logistic sigmoid: $σ (ξ) = \frac{1}{1 + e ^{- λ \cdot ξ}}$

Kde $λ$ je steepness parametr.
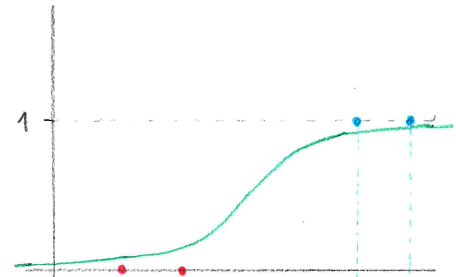
Hyperbolic tangens (tanh): $σ (ξ) = \frac{1 - e ^{- ξ}}{1 + e ^{- ξ}}$
Rectified Linear Unit (ReLU)

σ (ξ) = max (ξ, 0)

Důkazy

Boolovské funkce

Věta

Dvouvrstvý MLP, kde každý neuron má za $σ$ unit step function, je schopný spočítat libovolnou boolovskou funkci $F : {0, 1}^{n} \to {0, 1}$ .

Důkaz

Pro každý vstup $v = (v_{1}, ... v_{n}) \in {0, 1}^{n}$ takový, že $F (v) = 1$ , zkonstruujeme neuron $N_{v}$ jehož výstup bude 1, právě když jeho vstup je $v$ :

$w_{0} = - \sum_{i = 1}^{n} v_{i}$
$w_{i} = {1 - 1 v_{i} = 1 v_{1} = 0$

Všechny neurony $N_{v}$ zapojíme do jednoho neuronu, jenž počítá OR.

⁂

Podmnožiny vstupního prostoru (3 vrstvy)

Věta: Třívrstvý MLP, kde každý neuron má za $σ$ unit step function, dovede aproximovat libovolnou "rozumnou" podmnožinu vstupního prostoru.
Důkaz: Daná podmnožina se dá obalit hyperkostkami (t.j. čtverci 2D, kostkami ve 3D, …) — na to stačí dvě vrstvy (první udává nadroviny, druhá volí, která "strana" nadroviny ohraničuje hyperkostku). Třetí vrstva je pak OR, který spojuje hyperkostky nadefinované v prvních dvou vrstvách.

⁂

Podmnožiny vstupního prostoru (2 vrstvy)

Věta (Cybenko 1989): Dvouvrstvý MLP, kde každý hidden neuron má za $σ$ nějakou sigmoidal funcion, tedy platí:

$σ (ξ) = {10 ξ \to \infty ξ \to - \infty$

a pokud každý output neuron má lineární $σ$ , pak tato síť dovede aproximovat libovolnou "rozumnou" množinu $A \subseteq [0, 1]^{n}$ — tedy pro "většinu" vektorů $v \in [0, 1]^{n}$ platí, že $v \in A$ , právě když výstup sítě $> 0$ pro vstup $v$ .

⁂

Libovolná spojitá funkce (3 vrstvy)

Věta: Třívrstvý MLP, kde každý output neuron má lineární (pass-through) $σ$ a ostatní mají za $σ$ logistic sigmoid, dovede "spočítat" libovolnou funkci $f : [0, 1]^{n} \to [0, 1]$ . "Spočítat" zde znamená, že pro každé $v \in [0, 1]^{n}$ platí $∣ F (v) - f (v) ∣ < ε$ , kde $F$ je výstup sítě a $ε$ je povolená chyba.
Důkaz

⁂

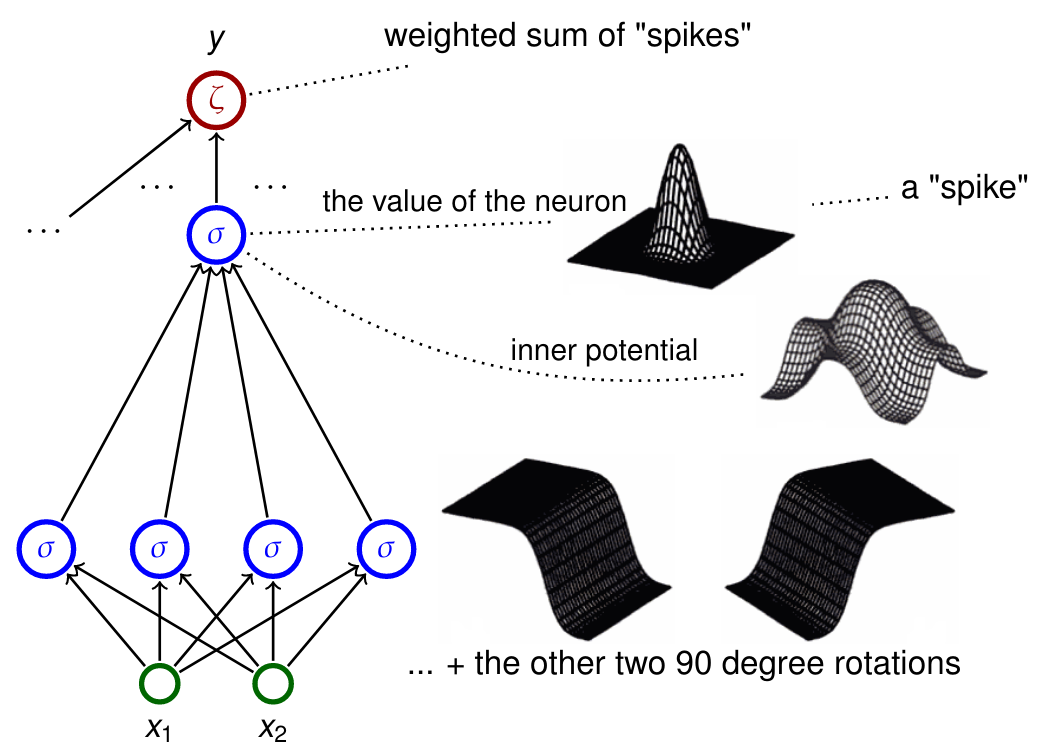
Libovolná spojitá funkce (2 vrstvy)

Věta (Cybenko 1989): To samé co věta výše, ale zvládl to jen se dvěma vrstvami.

Výpočetní síla

Uvažme neuronové sítě, které:

jsou rekurentní (mají cykly),
mají reálné váhy,
mají jeden input a jeden output neuron,
mají paralelní pravidlo pro výběr neuronů při výpočtu — všechny neurony se vyhodnotí v každém kroku,
mají aktivační funkci $σ (ξ) = ⎩ ⎨ ⎧ 1 ξ 0 ξ > 1; 0 \geq ξ \geq 1; ξ < 0.$

Slova $ω \in {0, 1}^{+}$ kódujeme jako reálná čísla následujícím způsobem:

δ (ω) = \frac{1}{2 ^{∣ ω ∣ + 1}} + i = 1 \sum ∣ ω ∣ \frac{ω ( i )}{2 ^{i}}

Warning

Takže např. z

ω = 101010

bude

δ (ω) = 0.101010 1

. Všimni si té zaražející jedničky na konci. Jak jinak bys poznal, že to slovo skončilo.

Síť rozpoznává jazyk $L \subseteq {0, 1}^{+}$ , pokud počítá funkci $F : A \to R$ , kde $A \subseteq R$ , takovou, že:

ω \in L ⟺ (δ (ω) \in A \land F (δ (ω)) > 0)

Note

Rekurentní neuronové sítě s racionálními vahamy jsou ekvivalentní Turingovým strojům.

Pro každý rekurzivně spočetný jazyk $L \subseteq {0, 1}^{+}$ existuje taková síť s méně než 1000 neurony, která jej rozpoznává.
Problém zastavení je nerozhodnutelný pro takové sítě s alespoň 25 neurony.
Existuje "univerzální" NN (stejně jako je "univerzální" TM).

Note	Rekurentní neuronové sítě s reálnými vahami jsou silnější než Turingovy stroje. Pro každý jazyk $L \subseteq {0, 1}^{+}$ existuje taková síť s méně než 1000 neurony, která jej rozpoznává.

Prakticky jsou ale takové sítě extrémně velké. Hodnota NN tak spočívá spíš v jejich schopnosti se učit, možnosti generalizace, robustnosti (chyby v inputu je jen tak nerozhodí) a masivní paralelizaci.