Convolutional Neural Networks (CNN)

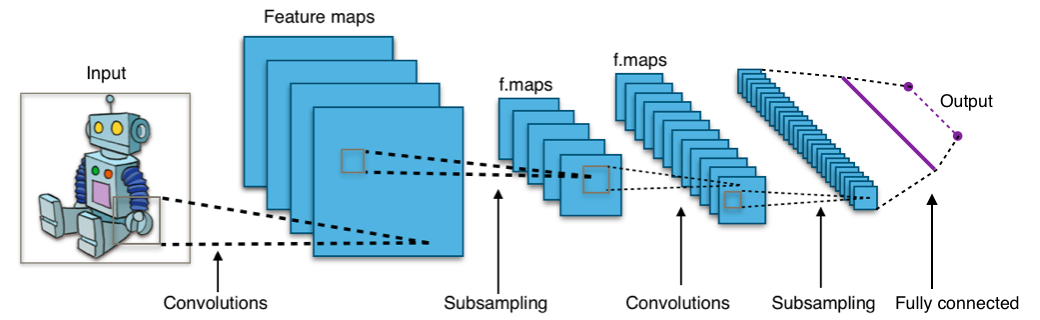
Konvoluční sítě jsou neuronky specializující se na obrázky. Mají nové typy vrstev: konvoluční a pooling.

Note	By Aphex34 - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=45679374

Přehled

Nové vrstvy
Notace
Trénink

Nové vrstvy

Konvoluční vrstva

Každý neuron je napojen jen na malý receptive field neuronů o vrstvu níže, který se posouvá o daný stride. Za to však všechny neurony v konvoluční vrstvě sdílí stejné váhy a biasy, což jim umožňuje naučit se nějaký vzor o velikosti receptive field — říkáme, že taková vrstva je feature mapa. Jelikož takových vzorů se chceme zpravidla naučit více, máme vícero vzájemně nezávislých feature map napojených na stejnou vstupní vrstvu.

Jinak jsou to ale staré dobré neurony s vnitřním potenciálem a aktivační funkcí.

Pooling vrstva

Nemají váhy. Slouží ke snížení počtu parametrů. Každý neuron počítá nějakou jednoduchou funkci na svém receptive field:

max-pooling — maximum,
L2-pooling — square root of sum of squares,
average-pooling — mean.

Notace

$X$ — množina input neuronů
$Y$ — množina output neuronů
$Z$ — množina všech neuronů
Neurony mají indexy $i$ , $j$ , …
$ξ_{j}$ — vnitřní potenciál neuronu $j$ po skončení výpočtu
$y_{j}$ — výstup neuronu $j$ po skončení výpočtu
$x_{0} = 1$ — hodnota formálního jednotkového vstupu (kvůli biasům)
$w_{ji}$ — váha spojení z neuronu $i$ do neuronu $j$ (dst ← src)
$w_{j 0} = - b_{j}$ — bias — váha z formální jednotky do neuronu $j$
$j_{\leftarrow}$ — množina neuronů $i$ , jenž mají spojení do $j$ (j ← i)
$j^{\to}$ — množina neuronů $i$ , do nichž vede spojení z $j$ (j → i)
$[ji]$ — množina spojení (dvojic neuronů) sdílících váhu $w_{ji}$

Trénink

Stochastic gradient descent můžeme mírně upravit a použit i na konvoluční sítě.Zvolme náhodně minibatch $T \subseteq {1, ..., p}$ z trénovacího setu $T$ . Za error function si volíme mean squared error:

E (w) = \frac{1}{p} k = 1 \sum p E_{k} (w)

SGD počítá posloupnost vah $w^{(0)}, w^{(1)}, ...$ .

Inicializujeme $w^{(0)}$ náhodně na hodnoty v okolí 0.
V kroku $t + 1$ vypočítáme:

$w^{(t + 1)} Δ w^{(t)} = w^{(t)} + Δ w^{(t)} = - ε (t) \cdot \frac{1}{∣ T ∣} k \in T \sum \nabla E_{k} (w^{(t)})$

Backpropagation

Pro dense vrstvy platí to samé, co u MLP:

\frac{\partial E _{k}}{\partial w _{ji}} = \frac{\partial E _{k}}{\partial y _{j}} \cdot σ_{j}^{'} (ξ_{j}) \cdot y_{i}

U konvolučních vrstev nestačí pro každou váhu $w_{ji}$ spočítat $\frac{\partial E _{k}}{\partial w _{ji}}$ , protože pro každou váhu existuje víc než jeden výstup $y_{j}$ . Tedy:

\frac{\partial E _{k}}{\partial w _{ji}} = r l \in [ji] \sum \frac{\partial E _{k}}{\partial y _{r}} \cdot σ_{r}^{'} (ξ_{r}) \cdot y_{l}

Předpokládejme dále, že error function je squared error. Pokud $j \in Y$ , platí:

\frac{\partial E _{k}}{\partial y _{j}} = y_{j} - d_{kj}

Pokud $j \in Z ∖ Y$ a $j^{\to}$ je dense nebo konvoluční vrstva, platí:

\frac{\partial E _{k}}{\partial y _{j}} = r \in j^{\to} \sum \frac{\partial E _{k}}{\partial y _{r}} \cdot σ_{r}^{'} (ξ_{r}) \cdot w_{r j}

Pokud $j \in Z ∖ Y$ a $j^{\to}$ je max-pooling, pak $j^{\to} = {i}$ a platí:

\frac{\partial E _{k}}{\partial y _{j}} = {\frac{\partial E _{k}}{\partial y _{i}} 0 pokud j = arg max_{r \in i_{\leftarrow}} y_{r} jinak

Note	Max-pooling nemá váhy, takže vzorec výše se zabývá vrstvou před max-poolingem, kde pouze neurony, jejichž index ( $arg max$ ) je index toho maximálního si zkopírují parciální derivaci z max-pooling vrstvy.