3D Models

Meshes

Manifolds

$n$ -manifold je prostor, kde okolí každého bodu je homeomorfní s $n$ -dimenzionálním Euklidovským prostorem.

Kružnice je 1-manifold. Koule je 2-manifold.

Interior tělesa

Body uvnitř tělesa.

Takové body, pro které platí, že otevřená koule (bez "obalu") s dostatečně malým poloměrem obsahuje jen body uvnitř tělesa.

Boundary tělesa

Body na hranici tělesa.

Takové body $q$ , pro které platí, že existuje takový bod $r$ , že všechny body mezi $q$ a $r$ (kromě $q$ , včetně $r$ ) jsou uvnitř tělesa.

Closure tělesa

Body, které nejsou vně tělesa:

closure (T) = interior (T) \cup boundary (T)

Regularized boolean operators

Booleanovské operace na tělesech, které eliminují "zbytky", které mohou vzniknout při booleanovských operacích.

A \cup^{*} B = closure (interior (A \cup B)) A \cap^{*} B = closure (interior (A \cap B)) A ∖^{*} B = closure (interior (A ∖ B))

Orientability

Dá se konzistentně rozhodnout, na které straně povrchu jsem v každém bodě?

Koule — ano.

Möbius strip — ne.

Boundary representation (B-rep)

Reprezentace tělesa jako množiny pospojovaných (orientabilních) povrchů, které tvoří boundary.

Topologie

Jak jsou povrchy pospojovaný dohromady?

Geometry

Kde ty povrchy vlastně jsou v prostoru?

Genus

"Kolik donutových děr to má?"

Maximální počet řezů podél uzavřených vzájemně se neprotínajících křivek, které nerozpojí těleso.

Euler characteristic (Euler-Poincaré formula)

Popisuje topologii nějakého prostoru nezávisle na tom, jak je zohybáný.

χ = V - E + F = 2 (c - g) + b

kde

$V$ je počet vertexů,
$E$ je počet hran,
$F$ je počet stěn,
$c$ je počet souvislných komponent,
$g$ je genus,
$b$ je počet boundary loops.

$E + 1 = V E^{'} + 1 = F E = E^{'} E + 2 = V + F V - E + F = 2$

Mesh representation

Strom solids → faces → edges → vertices.
Triangles (face set) — list of triangles with redundancy.
Indexed triangles — list of triangles with less redundancy.
Winged edge.
Half-edges.
Corner tables — tabulka rohů (vertex + trojúhelník).

Isotropic remeshing

Uniformizuje trojúhelníky.

Spočítej střední hodnotu délky hran (L).
Rozděl každou hranu, která je moc dlouhá (> 4/3 L).
Spoj každou hranu, která je moc krátká (< 4/5 L).
Flipni každou hranu, pokud to přiblíží stupeň vertexů k 6.
Posuň každý vertex směrem k průměru jeho sousedů (centroidu).

Subdivision

Parametric continuity

Popisuje, jak "pěkně" na sebe parametrické křivky navazují:

$C^{0}$ — obě křivky jsou spojité.
$C^{1}$ — obě křivky a jejich první derivace jsou spojité.
$C^{2}$ — obě křivky a jejich druhé derivace jsou spojité.

Geometric continuity

Křivka nebo povrch může mít $G^{n}$ kontinualitu. Pro segmenty křivky po obou stranách libovolného bodu $P$ :

$G^{0}$ — křivky se v $P$ dotýkají.
$G^{1}$ — křivky se v $P$ dotýkají a sdílí v něm tangentu.
$G^{2}$ — křivky se v $P$ dotýkají, sdílí v něm tangentu a střed křivosti.
…

Křivka je $G^{n}$ kontinuální, pokud se dá zapsat jako parametrická $C^{n}$ kontinuální křivka.

Typy vertexů

interior,
smooth boundary,
convex corner,
concave corner.

Subdivision scheme (refinement scheme)

Postup, podle kterého subdivizi křivky nebo povrchu provádíme. Schéma může být:

Approximating — přidá body do hran a existující body posouvá..
Interpolating — přidává nové body, ale prochází původními.
Corner-cutting — "seká rohy".

V případě povrchů je lze také dělit podle toho, jaká primitiva dělí:
Primal — dělí faces.
Dual — dělí vertices.

Subdivision Curves

Chaikin’s corner-cutting method (1974): Pro každý segment $\overline{P_{i} P_{i + 1}}$ lomené čáry $P_{1}, P_{2}, ..., P_{n}$ nahradí segmentem $\overline{Q_{i} R_{i}}$ , kde:

$Q_{i} = \frac{3}{4} P_{i} + \frac{1}{4} P_{i + 1} R_{i} = \frac{1}{4} P_{i} + \frac{3}{4} P_{i + 1}$
Bézier (De Casteljau) subdivision: Bézierovu křivku řádu $n$ můžeme rozdělit na dvě Bézierovy křivky řádu $n$ v kterémkoli bodě pomocí De Castaljau algoritmu. Není to interpolační schéma, jelikož (až na kraje) zahazuje kontrolní body.

Subdivision Surfaces

	Primal — triangles	Primal — quads	Dual
Aproximating	Loop	Catmull-Clark	Doo-Sabin, midedge, Dyn-Levin-Liu
Interpolating	Butterfly	Kobbelt

Primal — triangles

Primal — quads

Dual

Aproximating

Loop

Catmull-Clark

Doo-Sabin, midedge, Dyn-Levin-Liu

Interpolating

Butterfly

Kobbelt

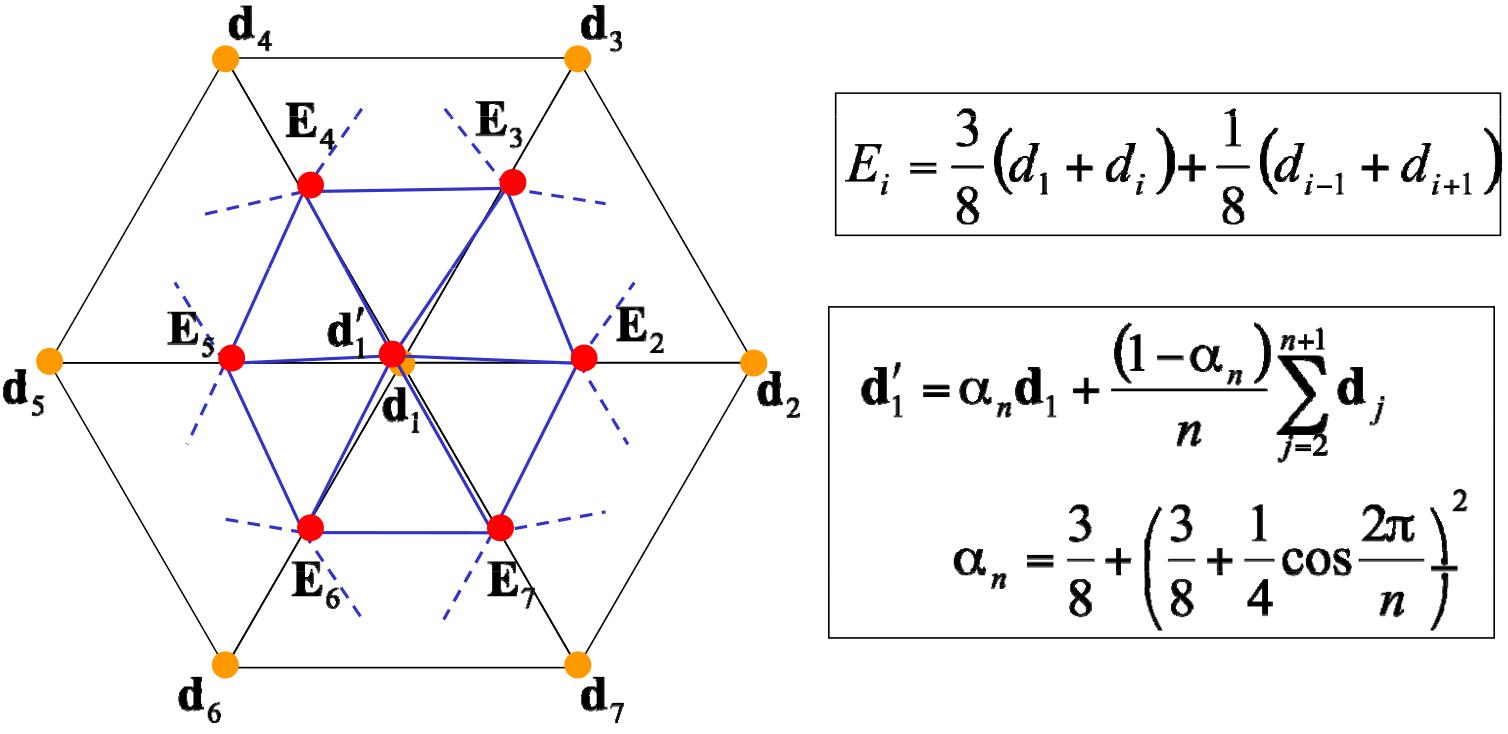
Regular B-spline subdivision

Podobně jako u Bézier subdivision pro křivky, můžeme složitě spočítat matici, která nám dá nové kontrolní body. Dá se to ale udělat i jednoduššeji:

f = \frac{v _{1} + v _{2} + v _{3} + v _{4}}{4} e = \frac{v _{1} + v _{2} + f _{1} + f _{2}}{4} v = \frac{f _{1} + f _{2} + f _{3} + f _{4} + 2 ( m _{1} + m _{2} + m _{3} + m _{4} ) + 4 p}{16}

kde pro 1 level subdivize musím spočítat 4 nové face pointy $f_{1}, ..., f_{4}$ , 4 nové edge pointy $e_{1}, ..., e_{4}$ a vertex point $v$ uprostřed nich.

regular b spline

Catmull-Clark Subdivision

Primal subdivision schéma. Generalizace regular B-spline subdivision pro iregulární (nemřížkové) meshe. Generuje $G^{2}$ souvislé limitní povrchy.

Pro každý face $i$ spočítej $f_{i}$ jako střední hodnota okolních vertexů.
Pro každou edge $i$ mezi $v_{j}, v_{k}$ oddělující faces $l, m$ spočítej $e_{i} = \frac{v _{j} + v _{k} + f _{l} + f _{m}}{4}$ .
Pro každý původní vertex $p$ spočítej nový vertex $v = \frac{F + 2 R + ( n - 3 ) p}{n}$ , kde:
- $n$ je valence vertexu (stupeň uzlu),
- $F$ je průměr nově vytvořených $f_{j}$ sousedících s $p$ ,
- $R$ je průměr midpointů všech hran dotýkajících se $p$ , kde midpoint je střed oné hrany ne ten nový edge point.
Spoj hranou každý nový face point s edge pointy hran, které tvořily ten face.
Spoj hranou každý nový vertex point s edge pointy hran, které vedly do původního vertexu.
Máš nové faces.

Note
By UserTwoSix - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=99207210, https://commons.wikimedia.org/w/index.php?curid=99207376

Loop Subdivision

Primal subdivision schéma pro trojúhelníkové povrchy. Generuje $G^{2}$ souvislé limitní povrchy.

loop

Butterfly Subdivision

Primal subdivision schéma pro trojúhelníkové povrchy. Generuje $G^{1}$ souvislé limitní povrchy.

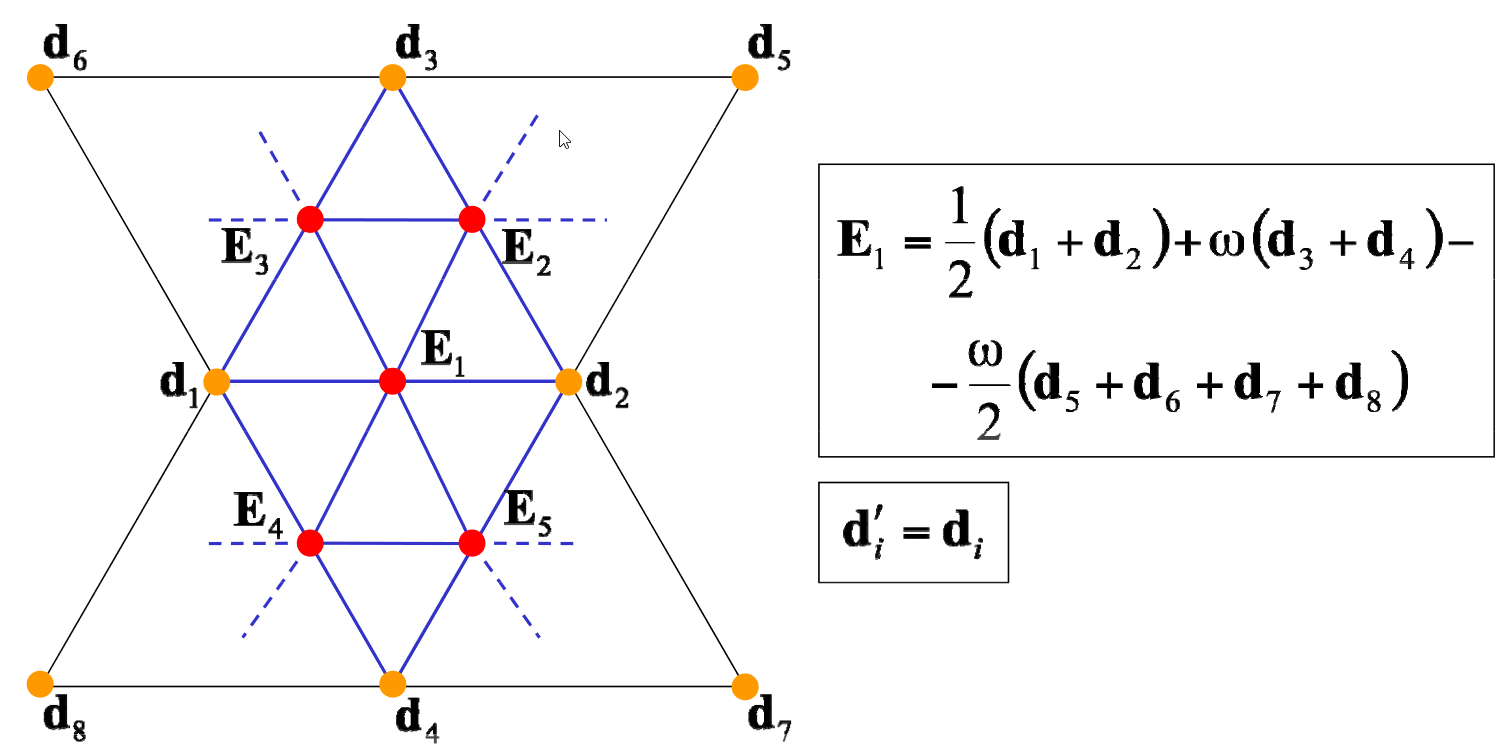
butterfly

"New points on edges, original points remain."

Doo-Sabin Subdivision

Duální subdivision schéma pro polygonální povrchy. Generalizuje bi-kvadratické B-spliny. Generuje $G^{1}$ souvislé limitní povrchy.

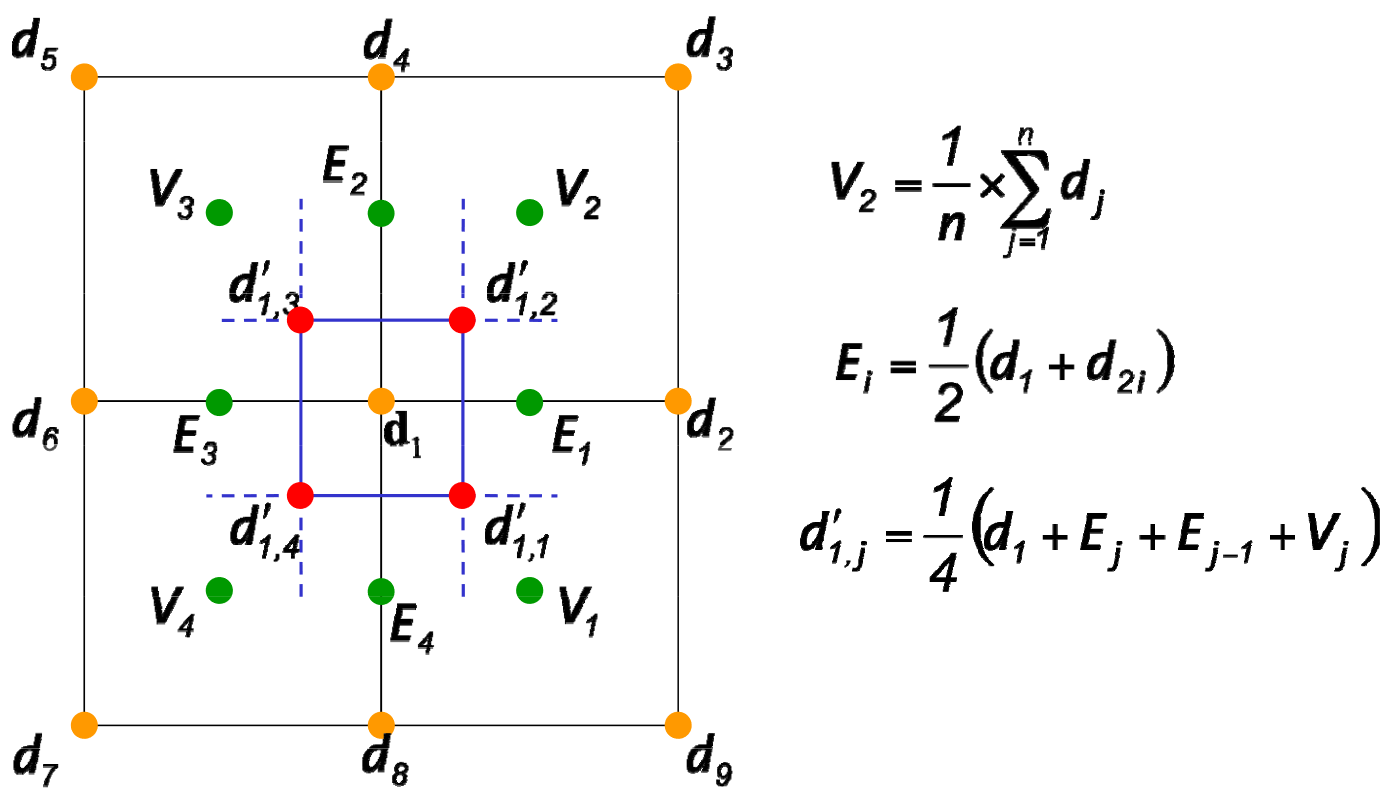
doo sabin

"A yellow replaced by 4 reds."

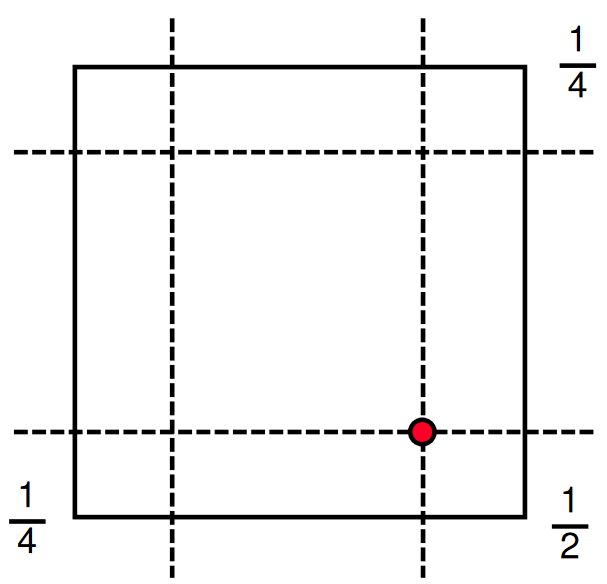
Midedge Subdivision

Duální subdivision schéma generující kvadrilaterální mesh.

midedge

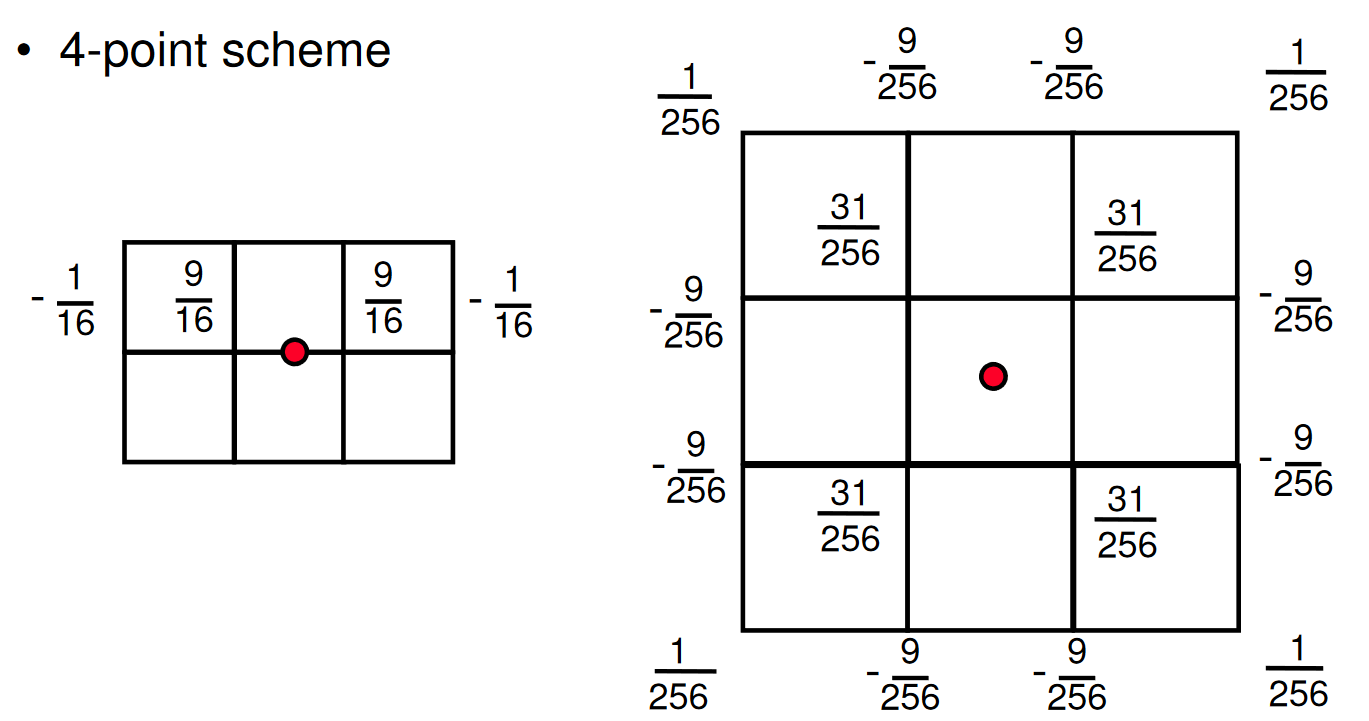
Kobbelt Subdivision

Primal subdivision schéma generující kvadrilaterální mesh.

kobbelt

Advanced modeling techniques

Barr’s global deformations

Scaling: $(X, Y, Z) = (s_{x} \cdot x, s_{y} \cdot y, s_{z} \cdot z)$
Tapering (zúžení): $(X, Y, Z) = (r_{x} \cdot x, r_{y} \cdot y, z)$
Twisting (podél z)
- $X = x \cdot cos (f (z)) - x \cdot sin (f (z))$
- $Y = x \cdot sin (f (z)) + y \cdot cos (f (z))$
- $Z = z$
Bending (podél y) pro bending range $(y_{min}, y_{max})$ , bending rate $\frac{1}{k}$ , center of the bend $y = y_{0}$ .

$y^{'} = ⎩ ⎨ ⎧ y_{min} y y_{max} y \leq y_{min} y_{min} < y < y_{max} y \geq y_{max} θ = k \cdot (y^{'} - y_{0}) X = x Y = ⎩ ⎨ ⎧ - sin θ (z - 1/ k) + y_{0} - sin θ (z - 1/ k) + y_{0} + cos θ (y - y_{min}) - sin θ (z - 1/ k) + y_{0} + cos θ (y - y_{max}) y_{min} \leq y \leq y_{max} y < y_{min} y > y_{max} Z = ⎩ ⎨ ⎧ cos θ (z - 1/ k) + 1/ k cos θ (z - 1/ k) + 1/ k cos θ (z - 1/ k) + 1/ k y_{min} \leq y \leq y_{max} sin θ (y - y_{min}) sin θ (y - y_{max}) y < y_{min} y > y_{max}$

Free-form Deformation (FFD)

Lokální deformace podle mřížky.

Umísti objekt, který chceš deformovat do mřížky (kostky či jiného konvexního objemu).
Transformuj "world" souřadnice $x, y, z$ na "lokální" souřadnice mřížky $s, t, u$ .
Modifikuj body mřížky dle libosti.
Transformuj objekt uvnitř mřížky zpět do "world" souřadnic.

Extended Free-form Deformation (EFFD)

Rozšíření FFD pro mřížky nesložené z rovnoběžnostěnů.

Axial deformations

Fáze I:

Měj původní křivku se začátkem a koncem.
Pro každý vertex objektu najdi nejbližší bod křivky.
V každém bodě křivky měj lokální souřadnicový systém (Frenetův rámec).

Fáze II:

Deformuj křivku, aplikuj změny.

Free-form Deformations with Catmull-Clark Volumes (CCV FFD)

Preprocessing fáze:

Oblast, kterou chceš deformovat obal mřížkou.
Subdividuj mřížku pomocí Catmull-Clark na $n$ kroků.
Každý vertex deformovaného objektu označkuj indexem buňky, ve které se nachází.
Parametrizuj vertex pomocí lokálních souřadnic $u, v, w$ buňky, ve které se nachází.

Deformační fáze:

Deformuj původní mřížku.
Subdividuj mřížku pomocí Catmull-Clark na $n$ kroků.
Pro každý vertex najdi podle značky jeho novou buňku a deformuj $u, v, w$ .

Sweep-based FFD: Modifikuje mesh přímo, ne skrze mřížku. Na řezy meshem aplikuješ afinní transformace.
Implicit surfaces: Objekty definované pomocí reálných funkcí. Normály lze získat gradientem. Dají se použít i v constructive solid geometry.
Blobs: Meshe popsané součtem Gaussových křivek.

Volume data rendering — surface reconstruction

Volume data visuliation

Aplikace při zpracování dat z Roentgenu, MRI, pozitronové emisní tomografie. Takže v medicíně, geologii, seismologii, meteorologii, matematice.

Formáty dat

Colinear Regular Grid
Colinear Irregular Grid
Grid with Regular topology
Hybrid grid
Voxels — hodnoty uprostřed buněk
Cells — hodnoty v mřížce

Iso-surface reconstruction

Výpočet a vykreslení povrchu, kde mají data stejné hodnoty. Mezi metody patří:

Non-transparent voxels
Iso-lines-based surface — spojování 2D iso-křivek
Marching cubes

Marching cubes

Mesh simplification

Nový vertex vznikne průměrováním okolí.

Quadric Error Metric (QEM) Simplification

Postupně smršťuj hrany (kratší než threshold) od té, která má nejmenší cenu. Cena se odvíjí od kvadratické chyby vzhldem k okolním trojúhelníkům.

Progressive meshes

Meshe, na kterých lze provádět operaci ecol (edge collapse) a její inverzi vsplit (vertex split). Používá explicit energy metric — součet vzdáleností mezi vertexy + penalta za počet vertexů + energie hran, kdyby to byly pružiny.

Geomorphs

Smooth přechody mezi dvěma progressive meshi.